Casino game expected value
New casino sites to play real money
Where EV is the expected value, x1 . Xn are possible outcomes and p1 . Pn are respective probabilities of the outcomes to happen. The expected value in poker works on the same principle as in the above-described exhibits. However there is one substantial difference – in poker you can influence by your decisions whether you will win or lose in a long-term period.
Expected value in gambling
The concept of expected value (EV) can be broadly utilized in gambling, but as well as in common life. It enables to optimize an outcome, or let us say, winning chances under the conditions of risk. By means of expected value we can determine long-term house advantage (or profit) of any wager in any casino game, but we can also maximize our winning chances in poker.
The word "expected" can be connected with other words like "outcome" or "return". It is necessary to emphasize that the expected value is related to a long period or a great number of random samples. The more samples – e.G. Number of spins in roulette or rounds in poker – the more likely the outcomes will approach the expected value.
Although the calculation of the expected value contains a bit of math and statistics, its principle is quite simple (which makes it even more powerful and beautiful) as it is clearly demonstrated on the exhibits below.
We mentioned the risk in the preface, let us define it. The risk is a possibility of deviation from the expected state (outcome, value). The risk, in contrast to uncertainty, can be measured by probability, e.G. We know what the probability to lose a stake is.
The uncertainty means that we do not know what will happen (the future is uncertain) and we do not know or we are unable to determine the probabilities of events. A little more theory and we can follow the exhibits below.
You might be interested in the use of expected value and risk in business and/or investments.
What is expected value
The expected value (EV) is a weighted average of all possible outcomes, whereas the weights are represented by probabilities. The expected value is a mean value, not necessarily the most probable outcome! The general formula of the expected value, EV , is the following:
Where EV is the expected value, x1 . Xn are possible outcomes and p1 . Pn are respective probabilities of the outcomes to happen.
The expected value can be both positive and negative. A rationally acting person makes such decisions where the expected value is positive and refuses those decisions that bring negative expected value.
However decisions with negative expected value can be admitted in case there is nothing better and we have to choose the lesser evil – we go for a decision with the least expected loss.
This strategy applies to poker and is the key to long-term success. In terms of casino games, whereas the result depends solely on chance, the expected value is (almost) always in player's disfavor – it secures casino's long-term profit.
House edge determination based on the expected value
The house edge comes from a difference between real and fair payout. The real payout (declared and paid out by a casino) is lower than the fair payout. The fair payout is such a one when the expected value (of a wager) is 0, in other words when casino's long-term profit is 0.
In the following exhibits we presume to bet one dollar. There are typically only two possible outcomes of a wager – either a win or a loss. The win is then one dollar times the payout and the loss is always the one dollar. We are able to determine the probabilities of winning and losing, therefore we can mark the following:
X1 = the first possible outcome = loss of 1 dollar,
p1 = probability of loss,
x2 = the second possible outcome = win (payout),
p2 = probability of win.
Exhibit 1: expected value of a single number bet in roulette
To remind: there are 18 red numbers, 18 black numbers and a zero in french roulette, that is 37 numbers in total. There is an extra number in american roulette – so called double zero – which makes the total of 38 numbers. First let us have a look and the variables and the calculation for the french roulette:
X1 = −1 (the loss of 1 dollar),
p1 = 36/37 (probability of loss: 36 out of 37 numbers lose),
x2 = 35 (payout 35:1),
p2 = 1/37 (probability of win: only 1 number out of 37 numbers wins).
A player's disadvantage (i.E. Negative expected value) = house advantage. In case of this single number bet, a casino has an edge over the player 2.7% – this is also the casino's long-term profit of the turnover on single number bets.
Let us see the expected value in the american roulette with a double zero, i.E. There is "only" one extra number, but the payout remains the same 35:1 as in the french roulette. Now 37 out of 38 numbers lose one dollar and only 1 number of of 38 numbers wins 35 dollars, so the expected value is then:
EV = (−1) × (37/38) + 35 × (1/38) = −0.0526 = −5.26% .
The house advantage of the single number bet in the american roulette is almost twice higher than in case of the french roulette(!) if you feel like playing roulette, which one of them will you choose?
Exhibit 2: expected value of even-money bets in roulette
Even-money bets are characterized by the payout 1:1. In roulette those are red/black, even/odd and high/low numbers. The following calculation applies to the french roulette. If you bet e.G. On the red color, then 18 numbers win and 19 numbers lose (black numbers and a zero lose).
EV = (−1) × (19/37) + 1 × (18/37) = −0.0270 = −2.7% .
Because some (especially european's) casinos allow to take back half of the bet (or they return it automatically) when a zero comes out, the expected value = player's expected loss = house advantage is only half too, thus 1.35% . Analogously we can calculate the house edge in the american roulette, which makes 5.26% again (the bet loses instantly when zero or double zero come out).
Expected value in poker
The expected value in poker works on the same principle as in the above-described exhibits. However there is one substantial difference – in poker you can influence by your decisions whether you will win or lose in a long-term period.
The good players accept those decisions that represent positive expected value. In all situation you can calculate or estimate whether it is worth betting: it depends on how and for how much you can improve your initial hand (or card combination if you like). This way of play is referred to as money to pot ratio and it is described on the 5-card stud poker page. It is an application of the expected value.
The expected value is positive if you can improve your hand (that can win the pot) for relatively low amount of money (you have to call other player's bets) – such decisions will pay off in the long run!
→ be sure to have a look at the poker variance and dollar EV adjusted. And then you may follow up with a simple example of variance calculation (based on two coin flipping games) and its detailed explanation. And finally do not miss the variance calculation for 9 player SNG.
On the other side the expected value is negative if a chance to improve one's hand (and to win the pot) is low or relatively lower than the amount of money that you have to put to the pot. You risk a lot to win a relatively small pot.
That is a wrong decision made by bad players, who risk in a disproportionate way relying on pure chance. It can lead to success short-term and you can beat a professional incidentally. However in a long period the outcomes are close to the expected value and only those can be successful who bear in mind the rule of expected value.
Expected value of a bet in casino games


What is expected value for casino games
Expected value is the long-run average value of repetitions of the experiment it represents. This we usually call simply as “expectation” and doesn’t tell us if and how much we can win or lose by a specific bet in a gambling game.
In gambling, by expected value or average expectation, we mean the calculation of how much money we will win or lose in the long run based on the odds and payouts of the game. Some clarifications are needed:
- The amount of money we should expect to win or lose is usually given as a percentage of the money wagered.
- By long run we mean after many thousands of trials. The more trials the closer we will get to the expected value prediction.
- This is a relatively accurate theoretical prediction of the long run result of our play, but still, actual results can vary.
The house edge of casino games
Naturally, all casino games have a negative expected value. All players are expected to lose in the long run. The games are designed in favor of the casino. Actually, the expected value of any casino games is equal (in a negative way) to the house edge – they are the same thing. Specifically here is the expected value or house edge of the main casino games:
- Roulette (double zero): -5,26%
roulette (single zero): -2,7%
roulette (even chance bets, single zero with la partage or en prison rule): -1,35% - Blackjack: -0,5%
- Caribbean stud poker: -5,22%
- Craps don’t pass: -1,36%
craps come: -1,41%
craps tie: -14,35%
craps pair: -10,36% - Baccarat banker: -1,05%
baccarat player: -1,2% - Video poker: -1% (varies – depends on the game)
- Slot machines: -10% (varies – depends on the game)
This negative expected value or house edge is the one and only reason that mathematicians claim that it is impossible to win a game of chance in the long run. I have explained with arguments my disagreement to this thesis, in the house edge monograph.
How to calculate the expected value of any game and any bet
Sometimes there can be special rules or maybe the is no fixed house edge. You can always calculate the probability and the expected value (negative house edge) of any bet by using the following equation:
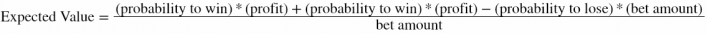
If we have multiple bets at the same time: we multiply the probability of our bets to win with their respective profits in case of win and we add them together. Then we deduct the probability to lose multiplied by the loss (which is our bet amount). Then we divide the sum to the amount of our bet.
If we only make one bet, then the equation is:
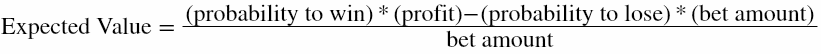
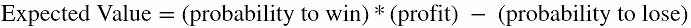
Dozen example
Now let’s calculate the expected value of the dozen bet in roulette. We already know (see previous section) that every bet in single zero roulette has an expected value (or house edge) equal to -2,7%, but let’s calculate it ourselves.
For a dozen, the probability to win is 12/37 because we are effectively betting on 12 numbers from 37 total numbers. The profit in case of win is 2 units. The probability to lose is 25/37, because 25 numbers out of 37 make us lose. So the expected value of the dozen bet is:
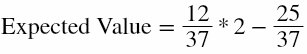
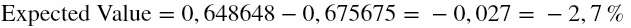
Which means that “in the long run” we expect to lose an amount equal to 2,7% of the total amount wagered.
Fantasy example
A question from our forum:
Let’s say the that I was playing the following numbers: 1-2-3-4-5-6-7-8-9-10 and was betting 1 chip on each number. Now the croupier congratulates me for my birthday and says “you can play two extra numbers where you don’t have to pay” and I add
11-12. So basically now I am playing 12 straight numbers for the price of 10. What would be my advantage?
Let’s calculate the expected value of this fantasy bet. We are betting 12 numbers with only 10 chips and each number pays 35 units profit. We have:
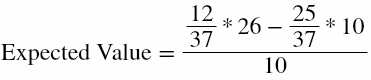
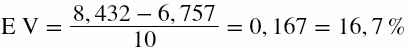
So instead of a -2,7% disadvantage, in this special example we have a 16,7% advantage.
With the equation presented in this article you can calculate the advantage or disadvantage of any random or lucky bet, if you know the probability of winning.
Casino math: expected value


For some time now I’ve been talking about advantage play and how part of the process is understanding how to tell when an opportunity exists. But it’s not always just about how many wilds and spins are available on scarab, or wild reels left behind on wheel of fortune.
Some advantage players take things a step further and attempt to calculate the expected value of an opportunity. In certain cases, it’s straightforward; in others, it can be somewhat complex math and observation.
It’s beyond the scope of this blog to share the complex scenarios – casual players will likely not play a game enough, nor wish to keep track of what’s necessary, to determine a specific play when it gets complicated. Given you also don’t know what payback a slot is set at, it’s a somewhat imprecise process because the same machine could pay or play somewhat differently at different casinos. So you’ll see me here talking about basic visual cues in most cases and leave it at that.
However, simpler expected value calculations can be done on some more obvious opportunities. That’s the purpose of today’s article.
Free bets/coupons on table games
One easy expected value opportunity is on table games. The pays are very clearly outlined, and the odds possible to calculate, because games are based on visual or concrete things. For instance, it’s not hard to know the exact house edge of a game of roulette, because all the pays, possible outcomes, and so on are very clearly outlined. Sames goes for blackjack, craps, baccarat… this is part of what makes certain games attractive to players.
So when you get an offer for a $25 free bet, for instance, and have to play it on an even money bet, you can figure out what your expected value would be. The simplest math on many even money bets is that you’ll win roughly half the time, and lose roughly half the time, so that’s about $12.50 for the expected value. But since casinos always build in a house edge, you know the expected value will be a touch less.
Now, that’s awfully imprecise, so you can do the homework online and see that a craps pass line bet has a low house edge, which means it’s closer to 50/50, vs. A roulette bet on, say, red vs. Black, which can have between a much higher house edge, especially when two or three zero (green) spaces are present on the wheel. Even a craps field bet, which is also even money and allowed for free bets often enough, has a higher house edge in most cases by far than the pass line. Similarly, a blackjack bet is on the low side, but the table rules will determine the actual expected payback, depending on the house edge.
Table games is a one shot bet for free bet wagers – so it’s (for the most part) double or nothing. That’s why expected value comes out to a little less than half; a bit more than half the time you’ll lose the bet, while a bit less than half the time you’ll double up.
The exception is blackjack, which has more push scenarios as well as the ability to potentially get 3:2 on a blackjack. But it’ll still average out to a bit less than half your free bet as the expected value, so it still works as a rule of thumb.
Finally, free bets are offered in coupon books like american casino guide and las vegas advisor. Even though you have to buy a book or membership, the expected value of the coupons in the book can well exceed the cost of the books. All you have to do is commit to hitting enough casinos that offer coupons to make it worth it. (if you’re visiting downtown/fremont st., that alone will likely do the trick.)
Free slot/video poker play
For slot free play, you can look at the casino house edge on the denomination of slot you’re going to play (which for some states is listed online, and averages/reporting available in some places) and do some quick math. But if you presume a 85-95% average payback based on denomination, that can at least give you a guide.
If you get $100 in free slot play and play it on pennies with an average payback of 88%, your expected value is $88 ($100x.88). You can so a similar calculation for video poker (which usually casinos also allow for free slot play), with the bonus that the pay tables are publicly listed on the machine, so like tables you know exactly the expected payout of this machine and can calculate accordingly.
Unlike a free bet, which is a one shot win or lose, with your one bet, you generally make multiple wagers to work through that free play. You could with that $100 make 100 $1 wagers, or 5 $20 wagers, or 400 $.25 wagers. Slots can also pay a handpay on a single wager or nothing on 10 wagers. As such, you can have wildly different outcomes, but in the long term, on average, it should, like all other wagers, approach the expected value.
Cash + comps
One other expected value calculation is the combined benefit of cash and comp earnings. Take a casino that offers a full pay video poker game like jacks or better, which pays roughly 99.5% over time. Now let’s assume you have a comp program that gives you a $1 in comps for every $500 you gamble. That’s a payback of .2% and a total with the cash earnings of 99.7%.
That means for every $1,000 you gamble, you should over the long haul get paid $997. Now in a given session you may lose $500 or win $1,000, but averaged out over hours of play and many thousands of hands that’s the expectation.
Now let’s say that casino does a comp multiplier day, where you get more comps back. If the casino runs a 3x promotion, it’s now increased the comp payback to .6%. Add that to the cash winnings and you’re eat 100.1% – play it in this scenario long enough and you should be a winner.
Casinos are of course aware of this, so they’ll take measures to counter things at times, like not offer full pay jacks or better, or do so on denominations where you can’t earn all that much (like limit it to quarters). Or they may exempt video poker from the multipliers, or comp earnings altogether.
Savvy players will always check the pay tables and the promotions in case the right positive expected value scenario. For true positive expected value scenarios it tends to work best with video poker and tables, because other games, like slots and keno, have such high house edges in most cases, it just can’t reach above it.
However, if you have two casinos near each other and one’s giving you a higher expected value, even if it’s negative, it may be worth playing there so your money will last longer. For instance, if a casino in a market like las vegas is offering a 10x promotion, it could be valuable.
How to calculate the expected value
:max_bytes(150000):strip_icc()/expected-5733972a5f9b58723d773687.png)
- Ph.D., mathematics, purdue university
- M.S., mathematics, purdue university
- B.A., mathematics, physics, and chemistry, anderson university
You're at a carnival and you see a game. For $2 you roll a standard six-sided die. If the number showing is a six you win $10, otherwise, you win nothing. If you're trying to make money, is it in your interest to play the game? To answer a question like this we need the concept of expected value.
The expected value can really be thought of as the mean of a random variable. This means that if you ran a probability experiment over and over, keeping track of the results, the expected value is the average of all the values obtained. The expected value is what you should anticipate happening in the long run of many trials of a game of chance.
How to calculate the expected value
The carnival game mentioned above is an example of a discrete random variable. The variable is not continuous and each outcome comes to us in a number that can be separated out from the others. To find the expected value of a game that has outcomes x1, x2, . . ., xn with probabilities p1, p2, . . . , pn, calculate:
For the game above, you have a 5/6 probability of winning nothing. The value of this outcome is -2 since you spent $2 to play the game. A six has a 1/6 probability of showing up, and this value has an outcome of 8. Why 8 and not 10? Again we need to account for the $2 we paid to play, and 10 - 2 = 8.
Now plug these values and probabilities into the expected value formula and end up with: -2 (5/6) + 8 (1/6) = -1/3. This means that over the long run, you should expect to lose on average about 33 cents each time you play this game. Yes, you will win sometimes. But you will lose more often.
The carnival game revisited
Now suppose that the carnival game has been modified slightly. For the same entry fee of $2, if the number showing is a six then you win $12, otherwise, you win nothing. The expected value of this game is -2 (5/6) + 10 (1/6) = 0. In the long run, you won't lose any money, but you won't win any. Don't expect to see a game with these numbers at your local carnival. If in the long run, you won't lose any money, then the carnival won't make any.
Expected value at the casino
Now turn to the casino. In the same way as before we can calculate the expected value of games of chance such as roulette. In the U.S. A roulette wheel has 38 numbered slots from 1 to 36, 0 and 00. Half of the 1-36 are red, half are black. Both 0 and 00 are green. A ball randomly lands in one of the slots, and bets are placed on where the ball will land.
One of the simplest bets is to wager on red. Here if you bet $1 and the ball lands on a red number in the wheel, then you will win $2. If the ball lands on a black or green space in the wheel, then you win nothing. What is the expected value on a bet such as this? Since there are 18 red spaces there is an 18/38 probability of winning, with a net gain of $1. There is a 20/38 probability of losing your initial bet of $1. The expected value of this bet in roulette is 1 (18/38) + (-1) (20/38) = -2/38, which is about 5.3 cents. Here the house has a slight edge (as with all casino games).
Expected value and the lottery
As another example, consider a lottery. Although millions can be won for the price of a $1 ticket, the expected value of a lottery game shows how unfairly it is constructed. Suppose for $1 you choose six numbers from 1 to 48. The probability of choosing all six numbers correctly is 1/12,271,512. If you win $1 million for getting all six correct, what is the expected value of this lottery? The possible values are -$1 for losing and $999,999 for winning (again we have to account for the cost to play and subtract this from the winnings). This gives us an expected value of:
(-1)(12,271,511/12,271,512) + (999,999)(1/12,271,512) = -.918
So if you were to play the lottery over and over, in the long run, you lose about 92 cents — almost all of your ticket price — each time you play.
Continuous random variables
All of the above examples look at a discrete random variable. However, it is possible to define the expected value for a continuous random variable as well. All that we must do in this case is to replace the summation in our formula with an integral.
Over the long run
It is important to remember that the expected value is the average after many trials of a random process. In the short term, the average of a random variable can vary significantly from the expected value.
Casino bonus strategy – how to beat online casino with expected value betting

Estimated reading time: 21 minutes
Expected value betting – casino bonus strategy introduction
Online casino has been growing rapidly supported by many reasons such as data below. Our aim of playing online casino is solely to make sure PROFIT by focusing on how to extract bonus from the casino sites as quickly & effectively as possible, with expected value betting;

Advantage gambling
With that said, allow me to reiterate that one of our policies is “betting on chance is for losers, stop gamble betting but bet on only +EV to win reliably“. It is effectively our way to promote responsible gambling. And we strongly support gambleaware being explained in about us.
We would like our readers to exploit such reliable money making opportunities as many as possible. We employ abundance of customized tactics to get maximum return from various online casino games & bonuses. This report instructing the fundamental casino strategy focusing on expected value betting is one of our efforts to achieve those visions.
On line casino markets
You must be amazed that currently 85 countries already legalized on-line gambling as seen below;

And online gambling market shows the big number of online gamblers & their average spending time per day as below image;

However, we’re still in the infant stage when it comes to the growth of online gambling. The below image shows rapid growth of the market but indicates that only 1% of the gamblers play online means it has still huge potential for further growth;

Harsh reality
The issue is player’s loss. According to the same source of the online gambling market growth the article says
The truth is, 80 percent of people who are involve on gambling failed to win and ends up empty pocket. As the experts say, the ratio between winning and losing at online gambling is like 1 is to 100. But if you feeling lucky today, get ready to rumble! The online gambling market growth
This is the sad truth, and we don’t want people to lose money at casinos especially for aussie & singaporean – why? See the data at the bottom of the report beat the bookies by knowing how your enemy makes money – secret of odds. We want you to make profit based on NOT by chance but on mathematical advantage.
How to use casino bonus for expected value betting?
Many people just spend & lose without knowing the real value of casino bonus. Allow me to reiterate that you can’t beat casino for long term due to the built-in house edge. However, when the bonus comes in, the rule of the game becomes different. Yes, we turn the casino’s bonus into real extra money.
As illustrated in the below image, casino offers several types of bonus. But we need to carefully select the ones which allow us to extract with risk free.

Casino bonus sign-up tactics
Before moving into further, for those who are seeking quick practical guide for the best casino sign-up strategy, see 5 most profitable casino sign up methods – stay away from no deposit bonus;

Casino expected value betting – simple math behind
Let’s move to the practical strategies.

Odds & house edge
Firstly, see the below info-graphics produced by casino UK that explains the meaning of the odds;

Casino house edge
All the casino games (with just 1 or 2 exceptions in video porker games) there is house edge that makes you certainly lose in long term. It’s not a sort of cheating or manipulation at all. Casino is a profit aiming business and it’s absolutely fair for them to set profit structure to cover their business cost & reasonable profit as any other usual business does. The below infographics (the same source) briefly explains how the house edge is built-in by using roulette case;

Remember, mathematically you can’t win casino for long term. I am saying long term. F or short term yes you have chances to win due to the variance which is a dependence on luck, that is so called gambling.
We’re not doing gambling but expected value betting. Therefore our aim is not beating the casino game but focusing on the extraction of the bonus where we have edge with positive EV (expected value). So, expected value betting is placing bet with positive EV. Let’s see a bit of mathematics behind our approach.
Expected value
There are several types of casino bonus as briefly said in the above. The point is we should know how much value each bonus has for us and we can judge based on the 1 simple indicator of EV (expected value).
Very quick explanation about EV. Expected value is a concept in probability describing the average outcome of a random event. Means it’s the basis of determining the long-term profitability of betting. Simply, positive +EV is profitable over the long term and the bigger the more profit.

If you started getting bored, skip this section and just remember the basic notion that you can’t beat math. Therefore as long as you take the offers with positive EV you will surely beat the casino in long term. So, you have to focus on how to achieve positive EV by learning the basic tactics of each game.
Casino game (EV) expected value
In calculating EV in casino games, you need 2 variables of;
- House edge
- Total wager amount you plan to bet
Let’s say you play blackjack of 3% house edge, and you wager £100 in total, you will theoretically lose £3. Variance plays a lot for small wager, it may not be £3 but much bigger or smaller. But when the wager amount (to be precise the number of playing games) becomes large such as £10,000 ( £10 x 1,000 times play), the loss will get closer to 3%.
Casino bonus EV

Finally, how we apply the calculation into bonuses. For EV calculation, we need 3 variables of;
- Bonus amount
- WR (wager requirements) – this is a key element for bonus clearance. Many casino give you very generous bonus such as “500% match to your deposit”, namely if you deposit £100, you will be given £500 instantly. However, you have to wager the 20X rollover on your deposit + bonus (this is called WR) before you can withdraw any of your balance. Means if you have £600 deposit & bonus, you have to bet £12,000 on casino games before you withdraw any money. Casino expects you to lose all the money before completing this WR.
- House edge
With that information, you can tell if any gambling bonus could be profitable or not with the following formula;
EV = bonus (£) – WR amounts (£) x house edge (%)
Let’s apply the above examples of 500% bonus by playing blackjack;
EV = £500 – (£12,000) x 3% = £140 so you have positive EV of £140, thus you are able to make expected velue betting from this offer. It means you will not lose but surely win long term as long as you keep taking this offer.
This is how you assess each bonus offer with the basic EV formula. We have customized value calculation methods for different bonus type based on the level of the risk / reward. Please see the bottom of this document to check the list of specific instruction on each bonus type.
Casino expected value betting – games to play
Specific step by step instruction on expected value betting

Go the guide to get real cash from extremely low risk casino easy bonus where you see the instruction using real examples of the offers.
Our primary objective is efficiently extracting casino bonus for busy people rather than enjoying playing games, it’s wise to focus on fewer games and get used to them. I list below 3 games simply because;
- The lowest or relatively low house edge
- By far the most popular with simple rules (especially slots)

The key tactics applying to all 3 games is to reduce the variance as much as possible and make your loss close to the house edge. Means basically you should play as many games as possible with minimum stake / game unless otherwise required.
1) blackjack
Key direction
Chose single deck rather than multiple deck. Because it improves your chance of getting blackjack hand (aside from the detail probability calculation, 8-deck game’s successful drawing of blackjack is 98% of the single-deck game). To determine the exact house edge you plan to play, go wizard of odds’ blackjack house edge calculator .
Playing tactics
Always use blackjack perfect strategy. It allows us to make the optimal decisions based on the cards we have and what the dealer is showing. See the below table that exhibits your action to be taken for every occasion. All you need to do is to keep the table while playing and follow it. Don’t misunderstand this is not a winning tactics but the best tactics to make your plays close to the lowest possible house edge (say down to around 0.3%). Means you will still not win for long term but ending up with the lowest house edge. Simply put, reducing variance is all about our objective in advantage play of bonus hunting and the blackjack’s very low house edge among all games makes perfect sense to do it.
For the specific instruction of how to play blackjack with the real example, go online casino risk free bonus clearing – no rollover requirement tactics.
2) roulette
Key direction
There are 2 main versions, european & american. Must chose european because the house edge is half of american as seen in the below illustration. European has only one “0" while american has two “0".

Play tactics
Basically bet on double, means the even money bets namely;
- Red or black
- Even or odd
- Low (1 – 18) or (19 – 36)
,because it is the lowest house edge.
Some casino prohibits you to keep playing the double bet during the WR stage. Then you may use treble bets, our specific instruction for each bonus case will explain the details.
3) slot machine
Remember the house edge is not as low as the table games. The reason why I list slot as one of the 3 selected games is based on the fact that slots are the undisputed kings of online casinos. It accounts around 70% of all gaming revenue. Besides, many casino bonus offers are with slot (restricted only to slot to claim bonus) such as “free spins”, therefore avoiding slot will miss many lucrative opportunities.
Key direction
Try to pick high RTP (return to players). RTP describes % pay back to players, so if it says 90%, meaning that over time the machine will keep about 10% of all money bet and will return the other 90% to players in wins. The % is just the flip side of house edge. You may evaluate the RTP % as;
Superb: 98% 93%
Most slots have the RTP listed in their game rules or pay tables, for example, betfair casino is as below;
Or just goggle with for example “ocean princess slot RTP" (ocean princess slot is 1 of the highest RTP slots with 99.1% RTP, just FYI). In case you can’t find RTP information, you may want to avoid that slot.
RTP tips

Play tactics
Just a common sense first, in slot game, you will only win payouts on lines that you bet on. If you only bet on 10 of 25 paylines and the winning combination falls on a line that you didn’t in fact bet on (or activate), you get nothing for that combination. Thus as a general rule of thumb, it is in the players’ best interests to activate all paylines on every spin. Not doing so could result in missing out on progressives or other big wins.

Having said and as the basic principle to reduce the variance applies, the general approach is;
- Select minimum stakes
- Select maximum lines
For the spoon-fed instruction of how to play slot with the real example, go 3 most popular casino games – technique to rake cash from risk free bonus.
I focused on 3 games in this document but from purely lowest house edge game, video poker & craps beat these 3 games. I also introduced basic tactics on poker, craps & baccarat as a spinoff document, if you’re interested, please access to smart ways to use top 3 lowest house edge games to extract casino bonus.
List of high RTP slots
For your convenience, some of the extremely low house edge slots of which RTP is over 99% are;
goblin’s cave (playtech) – 99.3% RTP reels/paylines: 3×3/3 min/max bet: £0.10/£5.00






However, you may not always find these slots in casino sites, or even if you find, some casinos limit the WR contribution or entirely exclude from the WR contribution.
Blood suckers (netent) – 97.6% RTP reels/paylines: 5×3/25 min/max bet: £0.01/£50.00



BTW, the RTP of the most popular slots you can find in almost every casino (excluding blockbuster title or celebrity such as the dark knight or michael jackson king of pop etc) are;
starburst (netent) – 96.1% RTP reels/paylines: 5×3/10 min/max bet: £0.10/£100.00


Just for your information.
EV maximiser – slot machine mathematical bet simulator
BTW, when it comes to the slot machine, there is an excellent simulator called EV maxmiser

the estimated value chance of busting profit per hour and average amount of wagering complete A slots machine database with over 800 machines including the house edge and variance level of each game
It’s a very useful tool and essential for casino bonus raking because many casino offers involve slot machines. Remember, this is an advanced strategy with high risk, so unless you feel comfortable, put it on back burner.
Expected value betting key process & tactics
Explanation of all methods, online casino bonus hunting

Here, let me list general process & tactics as follows;
- After you finish reading this document, suggest strongly go through 5 most profitable casino sign up methods – stay away from no deposit bonus to grab the overall sign-up prioritization & avoid missing juicy opportunities.
- Then, move to read smart ways to use top 3 lowest house edge games to extract casino bonus, which is a spin-off tactical paper of this document.

- Once you complete the above 2, you may want to start conquering the casino bonus based on the following instructions ;
- Start up with how to guarantee real cash from casino bonus cashback sitescheck the cashback site and chose the casino sites you can receive cashback by signing-up via cashback sites, which is completely risk free + guaranteed profit.

- After exploiting all the cashback sign-ups, move to no risk (if you still like NDB – no deposit bonus) / extremely low risk by learning below specific tactics & step-by-step instruction to rake the various bonuses;

Casino basic strategies – security & fairness
As the last strategy, but obviously not least, security is the utmost priority together with the fairness when you play online casino with real money.
Fairness is the point if the game is not manipulated by the site to let you lose with unreasonable house edge etc. All reputable online casinos need to use RNG (random number generation) that is an algorithms used in computing when an outcome needs to be as random as possible. One way to know if the particular casino site is fair and secure is to check if the casino has the ecogra seal of approval, or whether it bears the logo of some other independent auditing agency such as itech labs or GLI. Such information is usually displayed at the bottom of a casino’s website.

By clicking on the appropriate logo you can basically view the report and certification of the testing agency.
Finally, check a few facts of the online gambling – male vs female


Since the data source is different, the man / female rate number is slightly different from the previous image though the point is female outsmarts male in terms of the winning in gambling.
So, guys what do you say? It’s time for the man to regain the gambling pride while ladies want to make it better.
Bonus clearing is sure way to do it.
If you have any inquiry or need any help from us, please contact us anytime

Just in case, you have not accessed to the below free program, suggest do it now, you will not lose anything but only make profit;
Make £/€/$ 50,000 extra money on the side - free program

Comprehensive 3 chapters
- Chapter 1: change mindset - you never gamble
- Chapter 2: rationale & strategies to achieve the extra money target
- Chapter 3: ultimate extra money guide daily action planner phase 1 - 5 (list every opportunity with step by step instruction)
All are FREE now, hope you will be impressed with the quality of the program. Don't wait but start now while I can keep the program free!!

Expected value
When building an understanding of the mathematics of gambling, a key concept to understand is that of expected value, which, in the gambling context, relates to how well a player can expect to do in a particular casino game over a series of fixed bets, for example repeatedly betting £10 on black in roulette.
Calculation of expected value
The expected value of a particular gambling scenario is worked out as follows:
[(probability of winning) x (amount won per bet) + (probability of losing) x (amount lost per bet)]
To give an example, let’s say a player is playing roulette and wants to work out what the expected value of a certain bet – say £10 on black – over a period of time will be. The probability of winning (see the roulette mathematics page for more info on roulette probabilities) a bet on black is 18 in 38 and the probability of losing is therefore 20 in 38. The amount won per bet and lost per bet is the same (£10). If we substitute these figures into the equation above, we get:
(18/38) x 10 + (20/38) x (-10) = -0.526
This figure of -0.526 means that if a player makes a bet of £10 repetitively, he can theoretically expect to lose £.053 each time he makes a £10 bet. This loss is incurred because of the house edge that all casinos operate with, which ensures that they make a profit in the long-term.
Probability theory and expected value
To work out the expected value for a string of identical bets requires a knowledge of probability theory, since probabilities are an important part of the equation that is used to work out expected value. Probabilities can be expressed as odds (for example, one in five), or as a fraction (1/5) or as a percentage (20%) or as a decimal (0.2). The decimal version is the most mathematically common and is easiest to work with. To work out the probability of something, simply divide the total possibilities for a particular event occurring (such as landing on red in roulette) by the total number of outcomes that exist for a particular scenario (spinning the roulette wheel). So, in the example above, we would divide 18 by 38 and say that the probability of landing on red in any given spin of a roulette wheel is approximately 0.474, or around 47%.
Expected value: every casino game’s winning formula

If someone told me when I was a kid that studying math could make me rich, I would’ve subtracted that paper airplane from my hand and added some serious homework time into the equation. But no one did, really, and as far as I was concerned back then – math nerds weren’t cool! But like most of the other decisions I made in my younger days, this one came back to bite me in the ass soon enough. Expected value comes straight outa the math books of hustle college, and you’re about to find out why.

“1 + 1 = U & me, baby”
– coolest kid in school –
So how do I calculate expected value?
Hold on to your knickers. We’ll get to that in a second, but before we do let’s talk about why this number is the reason you could be homeless if you don’t play your cards right.
In 2015, a word association study involving approximately five thousand participants conducted by professors from the las vegas university’s hustlenomics department, determined that over 90% responded indicating the first word that comes to mind when they hear the word ‘casino’ is – ‘luck’.
Alright, I’m bluffing. There is no such university.
The point I’m making is not many people would immediately think of ‘mathematics’ when they hear ‘casino’. And actually, that’s really all there is to it.

You can bet on it
When you place a bet, everything boils down to expected value. At least it should, because that’s how casinos make money from you. So what exactly is expected value? Simple:
“the expected value (EV) is an anticipated value for a given investment at some point in the future. In statistics and probability analysis, the expected value is calculated by multiplying each of the possible outcomes by the likelihood each outcome will occur, and summing all of those values.” – investopedia

Oh chillax. Obviously I’m going to explain. Expected value is actually a pretty simple concept to grasp. All it does is use probability theory to break down your ‘average’ win/lose to give you a mathematical determination of exactly how much you’re making or losing on that bet (ie. Your win/lose rate in the long run). So if your bet delivers positive expected value, you will make a profit in the long run and theoretically it is a good bet – and vice versa. See the example below and it should make perfect sense.
Here’s an example of expected value calculation
Think of someone you know who you consider to be a complete moron. Got it? Ok good. So one day, you and this idiot friend decide to wager on coin flips. Turns out your friend, being such a dumb ass, agrees to pay you $2 every time the coin flips heads while you only need to pay him $1 if it lands on tails. Common sense will tell you to take this bet, and so will expected value:
The odds of winning/losing are 50/50. If you chart the results out over a decent sample size of flips, the results will no doubt reflect that. Assuming this bet pays $2 to $1 – the expected value will be neutral (0). That means if you bet $1 and receive $2 (your original bet of $1 + a $1 win) when you predict the correct outcome – you will not make any money in the long run simply because 50% of the time you will lose your original bet of $1 while the other 50% of the time you will be returned $2. I hope I haven’t lost you. Read it again if you need to but make sure you totally get this, because it’s important.
Now let’s go back to the fun little game with your friend. Again, the odds of winning/losing are 50/50. However, this time round, each time you place a bet you pay $1 when you lose but receive $3 (your original bet of $1 + a $2 win) when you win. So how do you calculate the expected value? You simply multiply the probability and value for each outcome and sum them up like this:
[(probability of you winning) x (amount you will win)] + [(probability of you losing) x (amount you will lose)]
Which in this example will be:
Probability of winning = 0.5
probability of losing = 0.5
amount you will win = $3
amount you will lose = $1
(0.5 x 3) + [0.5 x (-1)] = 1
So because the end result is a positive number (+1), this bet has positive expected value (or as the cool casino nerds usually write it, “+EV”).
Expected value
Each session of play at a casino entails a certain amount of risk. In general, casino games are structured so that a low degree of risk usually results in small returns on investment or relatively harmless losses, while a greater level of risk may bring about some spectacular successes and failures. Players will typically wager only on games in which the potential rewards seem to warrant the risk required. They must therefore have some idea of how much can be won or lost relative to the cost of play—what gamblers call an “expected value” (EV).
Calculating EV
One way to think of EV is as a player’s predicted future gain or loss, or a representation of how much one expects to win or lose, if bets with identical odds are repeated many times. Mathematically speaking, EV is “the sum of the probability of each possible outcome of a wager multiplied by its payoff (value).”
A simple example of this is a coin toss in which calling the outcome correctly, heads or tails, results in a payout of 1-to-1 or “even money.” no matter whether the player calls heads or tails, the EV will always be the same. There are only two possible outcomes, each with the same probability of occurrence (1 in 2). The player can thus expect to be correct half of the time and wrong half of the time, so where “B” is the amount bet
In other words, the player’s forecasts result in an expected value of zero. Over the course of many, many flips, the number of heads occurring should be roughly equal to the number of tails, and the player can expect to break even, neither winning nor losing.
Any game of this sort, in which the player’s EV is zero (no net gain or loss), is called a “fair game.” note that “fair” in this case does not refer to the game’s technical process but to the house and the player having exactly the same likelihood of winning/losing.
Applying EV to casino games
According to this definition of “fair game,” the vast majority of gambling opportunities offered by casinos are not truly “fair.” they do not give the player an equal chance of winning. Instead, they favor the house and result in a negative EV for the player.
More specifically, over the long term, the player’s EV for any game or given wager will tend to approximate the house edge. In a game like american roulette, where the house has a built-in advantage of 2-in-38 on every spin, the EV for the player is -0.0526. That means the player can expect to lose roughly a nickel on every dollar wagered. For baccarat, the house edge is 1.06%
1.24%, so the player can plan on losing about penny out of every dollar.
However, casino games are not simply pure applications of probability calculus. Calculations of long-term results are not always reflected in short-term outcomes. Plus there is a human factor involved, and the progress of many games can be influenced by the action of the players.
Blackjack is a case in point. Each choice to hit, stand, double down, split, surrender or take insurance comes with its own expected value. Players who master basic strategy greatly improve their EV in general, and a card counter at the blackjack table can often identify situations where the house edge is negative and the EV is positive.
In fact, the house has an advantage of 4% or more for about one third of all blackjack deals, while the player has a positive EV of 0.04 or higher for another third of the hands. By skillfully increasing or decreasing one’s bets at the appropriate times, it is possible to win with mathematical certitude in the short term.
Likewise, video poker can offer a positive EV under certain circumstances. It has been shown that the game called “full pay deuces wild” gives the player a positive EV of 0.0076 when the optimum card selection strategy is applied. The same can be said of playing progressive slot games only when the jackpot is big enough or knowing when to raise in a game of caribbean stud. This is where human skill overcomes the randomness inherent in games of chance, improving the player’s expected value.
Casino math: expected value


For some time now I’ve been talking about advantage play and how part of the process is understanding how to tell when an opportunity exists. But it’s not always just about how many wilds and spins are available on scarab, or wild reels left behind on wheel of fortune.
Some advantage players take things a step further and attempt to calculate the expected value of an opportunity. In certain cases, it’s straightforward; in others, it can be somewhat complex math and observation.
It’s beyond the scope of this blog to share the complex scenarios – casual players will likely not play a game enough, nor wish to keep track of what’s necessary, to determine a specific play when it gets complicated. Given you also don’t know what payback a slot is set at, it’s a somewhat imprecise process because the same machine could pay or play somewhat differently at different casinos. So you’ll see me here talking about basic visual cues in most cases and leave it at that.
However, simpler expected value calculations can be done on some more obvious opportunities. That’s the purpose of today’s article.
Free bets/coupons on table games
One easy expected value opportunity is on table games. The pays are very clearly outlined, and the odds possible to calculate, because games are based on visual or concrete things. For instance, it’s not hard to know the exact house edge of a game of roulette, because all the pays, possible outcomes, and so on are very clearly outlined. Sames goes for blackjack, craps, baccarat… this is part of what makes certain games attractive to players.
So when you get an offer for a $25 free bet, for instance, and have to play it on an even money bet, you can figure out what your expected value would be. The simplest math on many even money bets is that you’ll win roughly half the time, and lose roughly half the time, so that’s about $12.50 for the expected value. But since casinos always build in a house edge, you know the expected value will be a touch less.
Now, that’s awfully imprecise, so you can do the homework online and see that a craps pass line bet has a low house edge, which means it’s closer to 50/50, vs. A roulette bet on, say, red vs. Black, which can have between a much higher house edge, especially when two or three zero (green) spaces are present on the wheel. Even a craps field bet, which is also even money and allowed for free bets often enough, has a higher house edge in most cases by far than the pass line. Similarly, a blackjack bet is on the low side, but the table rules will determine the actual expected payback, depending on the house edge.
Table games is a one shot bet for free bet wagers – so it’s (for the most part) double or nothing. That’s why expected value comes out to a little less than half; a bit more than half the time you’ll lose the bet, while a bit less than half the time you’ll double up.
The exception is blackjack, which has more push scenarios as well as the ability to potentially get 3:2 on a blackjack. But it’ll still average out to a bit less than half your free bet as the expected value, so it still works as a rule of thumb.
Finally, free bets are offered in coupon books like american casino guide and las vegas advisor. Even though you have to buy a book or membership, the expected value of the coupons in the book can well exceed the cost of the books. All you have to do is commit to hitting enough casinos that offer coupons to make it worth it. (if you’re visiting downtown/fremont st., that alone will likely do the trick.)
Free slot/video poker play
For slot free play, you can look at the casino house edge on the denomination of slot you’re going to play (which for some states is listed online, and averages/reporting available in some places) and do some quick math. But if you presume a 85-95% average payback based on denomination, that can at least give you a guide.
If you get $100 in free slot play and play it on pennies with an average payback of 88%, your expected value is $88 ($100x.88). You can so a similar calculation for video poker (which usually casinos also allow for free slot play), with the bonus that the pay tables are publicly listed on the machine, so like tables you know exactly the expected payout of this machine and can calculate accordingly.
Unlike a free bet, which is a one shot win or lose, with your one bet, you generally make multiple wagers to work through that free play. You could with that $100 make 100 $1 wagers, or 5 $20 wagers, or 400 $.25 wagers. Slots can also pay a handpay on a single wager or nothing on 10 wagers. As such, you can have wildly different outcomes, but in the long term, on average, it should, like all other wagers, approach the expected value.
Cash + comps
One other expected value calculation is the combined benefit of cash and comp earnings. Take a casino that offers a full pay video poker game like jacks or better, which pays roughly 99.5% over time. Now let’s assume you have a comp program that gives you a $1 in comps for every $500 you gamble. That’s a payback of .2% and a total with the cash earnings of 99.7%.
That means for every $1,000 you gamble, you should over the long haul get paid $997. Now in a given session you may lose $500 or win $1,000, but averaged out over hours of play and many thousands of hands that’s the expectation.
Now let’s say that casino does a comp multiplier day, where you get more comps back. If the casino runs a 3x promotion, it’s now increased the comp payback to .6%. Add that to the cash winnings and you’re eat 100.1% – play it in this scenario long enough and you should be a winner.
Casinos are of course aware of this, so they’ll take measures to counter things at times, like not offer full pay jacks or better, or do so on denominations where you can’t earn all that much (like limit it to quarters). Or they may exempt video poker from the multipliers, or comp earnings altogether.
Savvy players will always check the pay tables and the promotions in case the right positive expected value scenario. For true positive expected value scenarios it tends to work best with video poker and tables, because other games, like slots and keno, have such high house edges in most cases, it just can’t reach above it.
However, if you have two casinos near each other and one’s giving you a higher expected value, even if it’s negative, it may be worth playing there so your money will last longer. For instance, if a casino in a market like las vegas is offering a 10x promotion, it could be valuable.
Beejack
Languages
Expected value in casino games
Our recommended casinos
People often make a big deal about the house edge in casino gaming because it represents their relative chances of winning money. For example, french roulette carries a potential house edge of 1.35%, which is pretty low when compared to most games.
Interestingly enough though, the subject of expected value isn't discussed quite as much when it comes to casino games. But as you'll find out, expected value is just as important when trying to determine how much money you can win while playing certain games.
Expected value definition
Expected value (EV) is how much money you can expect to win or lose with each bet. In order to find out the expected value of each wager, it's important to know the house edge of the games you play.
Using the aforementioned 1.35% french roulette house edge, your expected value would be 0.9865 (1.00 - 0.0135). Assuming you made a $5 french roulette wager, your EV in terms of dollars would be -$0.07 [($5 x 0.9865) - $5]. As you can see, your expected value for each french roulette bet is negative.
Why play negative expected value games?
Seeing as how many casino games have a negative expected value, some people wonder what the point in gambling is. After all, the casino will win over the long-term in most games. But this is exactly the point because players can beat casinos over the short-term.
Calling upon french roulette once more, you stand to lose $0.07 with every $5 wager you make. However, this is an extremely small edge when you consider the size of the bet; in other words, you are dealing with an almost equal chance of making profits with every wager made.
Positive expected value games
What's nice is that there are actually a few casino games where players have positive expected value with each bet. Video poker is one game where this is the case because certain versions of deuces wild (100.8%) and double bonus (100.2%) poker give players a chance to win long-term money.
To illustrate how this works, let's say that you play a deuces wild game with 100.8% payback; in this case, your expected value would be 1.008. So if you made a $5 wager here, your expected value would be $0.04 [($5 x 1.008)) - $5]. Of course, it's also important to realize that you need to use excellent video poker strategy to get this positive expected value.
Some other positive expected value casino games that you might consider taking a look at include poker and blackjack (when card counting is involved). But just like with video poker, you need to be very skilled at these games to take advantage of the positive expected value.
So, let's see, what we have: the expected value is a powerful tool to determine house advantage (a player's disadvantage) of any wager in any casino game, but it is also essential for mathematically perfect play of poker. At casino game expected value
No comments:
Post a Comment